預金やローンの契約書を見ると、必ず出てくる「金利」という言葉。多くの人にとって、金利は身近でありながら、その仕組みや計算方法はよくわからないものかもしれない。
しかし、金利の基本を理解していないと、預金の選び方を間違えたり、ローンで思わぬ負担を抱えたりするリスクがある。金利の仕組みや計算方法を正しく理解すれば、より賢明な金融判断ができるようになる。
この記事では、金利の基礎知識を初心者にもわかりやすく解説する。利息の仕組みから計算方法まで、具体例を交えて徹底的に説明していく。これらの知識を身につければ、日々の家計管理から長期的な資産形成まで、幅広い場面で活用できるだろう。
金利の基本的な仕組み
家計管理において、金利の基本的な仕組みを理解することは重要である。ここでは、金利の仕組みについて説明する。

専門家のワンポイントアドバイス:
金利は経済指標の一つです。日本銀行の政策金利の動向にも注目しましょう。
金利とは?
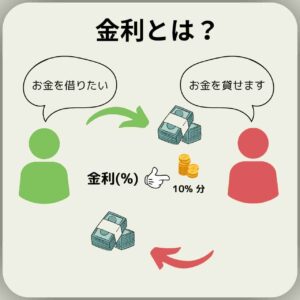
金利とは、お金を借りたときに払う追加の金額(利子)の割合のことである。この追加の金額を利息とも呼ぶ。つまり、借りたお金に対して、どれくらいの利子や利息を支払うかを示す割合が金利である。
たとえば、1万円を借りて、後で1万100円返すとする。このとき、追加で支払う100円が利子(または利息)である。金利は通常、パーセントで表される。この例では、金利は1%(100円÷1万円×100)となる。
お金を借りる人は金利に応じた利子を支払い、お金を貸す人は利息を受け取る。これが金利の基本的な仕組みである。
金利の役割

金利には大きく分けて2つの役割がある。
ひとつ目は、時間とお金の価値を調整することである。今すぐ使えるお金は、将来もらえるお金よりも価値がある。金利は、この時間の差を埋める役割を果たす。たとえば、定期預金で1年後に利息がつくのは、1年間お金を使えなかった分の調整といえる。
ふたつ目は、お金の需要と供給のバランスを取ることである。たとえば、金利が高くなると、お金を借りる人が減り、貸す人が増える。逆に、金利が低くなると、借りる人が増え、貸す人が減る。住宅ローンの金利が下がると住宅購入が増えるのは、いい例である。
利息の計算方法:単利と複利の違い
利息の計算方法には、おもに単利と複利の2種類がある。これらの違いを理解することは、預金や投資、ローンなどの金融取引を行ううえで非常に重要である。ここでは、単利と複利それぞれの仕組みと計算例を説明する。
| 単利 | 複利 | |
|---|---|---|
| 利息の計算方法 | 元本に一定の金利を乗じて計算 | 一定期間ごとに 利息を元本に組み入れて計算 |
| 利息の受取方法 | 元本とは別に受け取る | 元本に加算される |
| 長期的な収益 | 複利よりも低い | 単利よりも高い |
単利の仕組みと計算例
単利とは、元本に対してのみ利息が発生する計算方法である。単利では、利息が元本に加算されることなく、毎回同じ金額の利息が発生する。
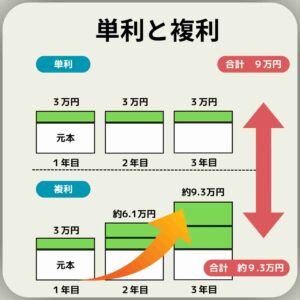
たとえば、100万円を年利3%で3年間、単利で運用した場合を考えてみよう。
- 1年目:100万円 × 3% = 3万円の利息
- 2年目:100万円 × 3% = 3万円の利息
- 3年目:100万円 × 3% = 3万円の利息
3年後の合計金額は、元本100万円 + 利息9万円(3万円 × 3年)= 109万円となる。
複利の仕組みと計算例
複利とは、前の期間に発生した利息を元本に加えて、次の期間の利息を計算する方法である。複利では、利息が元本に加算されるため、時間が経つほど利息が大きくなる。
先ほどと同じく、100万円を年利3%で3年間、今度は複利で運用した場合を見てみよう。
- 1年目:100万円 × (1 + 3%) = 103万円
- 2年目:103万円 × (1 + 3%) = 106.09万円
- 3年目:106.09万円 × (1 + 3%) = 109.2727万円
3年後の合計金額は約109.2727万円となり、単利の場合よりも0.2727万円多くなる。
長期間の運用では、この差がさらに大きくなるため、複利の効果は無視できない。たとえば、老後の資産形成を考える際には、複利の効果を活用することが重要である。

専門家のワンポイントアドバイス:
複利の効果を実感するには、長期的な視点が重要です。若いうちから資産運用を始めることをおすすめします。
預入期間と利息計算方法の関係
預金の利息計算は、預入期間によって異なる方法が適用される。ここでは、預入期間が利息計算にどのような影響を与えるのか、また、年利・月利・日割り計算の違いについて説明する。
預入期間が利息計算に与える影響
預金の期間は、短期と長期に大きく分けられる。短期の預金(通常1年未満)と長期の預金(1年以上)では、利息の計算方法が異なることがある。
短期の預金では、月利や日割りで利息が計算されることが多い。一方、長期の預金では、年利で利息が計算されることが一般的である。
たとえば、1年未満の定期預金では、預入期間に応じて日割りで利息が計算されることがある。これに対し、1年以上の定期預金では、年利をもとに複利で計算されることが多い。
年利と月利、日割りの違い
年利、月利、日割りは、それぞれ異なる期間を基準に利息を計算する方法である。
年利は、1年を基準として利息を計算する。たとえば、年利2%の預金では、1年間で元本の2%の利息がつく。
月利は、1ヶ月を基準として利息を計算する。年利を12で割ることで、月利を求めることができる。たとえば、年利2%の場合、月利は約0.167%(2%÷12)となる。
日割り計算は、預入日数に応じて利息を計算する方法である。日割り計算は、中途解約時や短期の預金で多く使用される。
たとえば、年利2%の預金に100万円を180日間預けた場合、日割り計算では以下のように利息が計算される:
100万円 × 2% × (180日 ÷ 365日) ≒ 9,863円
このように、預入期間と計算方法の違いにより、実際に受け取る利息額が変わってくる。預金商品を選ぶ際は、金利だけでなく、預入期間と利息計算方法も確認することが大切である。
金利・利回り・利子・利息の特徴と違い
金融に関する用語には、似たような言葉が多く存在する。ここでは、金利・利回り・利子・利息という4つの用語の特徴と違いについて解説する。これらの違いを理解することで、金融商品の特徴をより正確に把握できるようになる。
金利・利回り・利子・利息の意味
金利、利回り、利子、利息はそれぞれ異なる意味を持つが、密接に関連している。それぞれの特徴をまとめると以下のようになる。
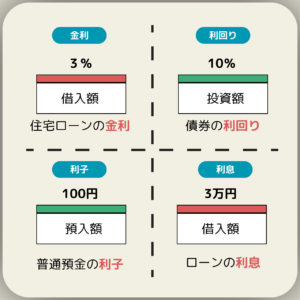
- 金利:お金を借りる際に支払う、または預ける際に受け取る利息の割合のことである。金利は通常、年率で表示され、金融取引の基本となる重要な指標である。たとえば、年利1%の預金では、1年間で元本の1%の利息がつく。
- 利回り:投資によって得られる収益率のことを指す。金利と似ているが、より広い概念である。利回りには、債券や株式の配当など、金利以外の収益も含まれる。たとえば、10万円で購入した債券から年間1万円の利子を得た場合、利回りは10%(1万円÷10万円×100)となる。
- 利子:お金を借りたり預けたりする際に、元本に対して支払われる、または受け取る金額のことである。利子は金額で表され、金利を元本に掛けて計算される。
- 利息:利子と同じ意味で使われることが多いが、厳密には預金や貸付金から生じる収益を指す。ローンの場合は利息、預金の場合は利子と使い分けることもある。
これらの用語は、金融取引において重要な役割を果たしている。預金者にとっては、金利や利回りが高いほど有利であり、借り手にとっては、金利や利子が低いほど有利になる。また、税金の存在により、税引き前と税引き後で金利や利息に差が生じるため、実質的な収益や負担を把握することが重要である。
金利・利回り・利子・利息の違い
それぞれの特徴を解説したが、もう少し違いがわかるよう、金利・利回り・利子・利息の特徴をまとめると、次のようになる。
- 金利
- 定義:元本に対する利息の割合を表す指標
- 説明:金融機関が預金や貸出に対して適用する利率のこと
- 例:年利0.1%の定期預金の金利は0.1%
- 利息
- 定義:元本に金利を乗じて計算される金額
- 説明:預金や貸出に対して支払われる金額のこと
- 例:100万円を年利0.1%で預けた場合の利息は、100万円 × 0.1% = 1,000円
- 利回り
- 定義:投資による収益率を表す指標
- 説明:元本に対する収益の割合を示し、金利だけでなく、値上がり益なども含めて計算される
- 例:100万円を年利0.1%の定期預金に預けた場合、税引き前の利息は1,000円(100万円×0.1%)となる。ただし、利息には20.315%の税金がかかるため、税引き後の利息は797円(1,000円-203円)となる。この場合、税引き後の利回りは0.0797%(797円÷100万円×100)である。
- 利子
- 定義:お金を借りた際に支払う対価
- 説明:利息と同じ意味で使われることが多いが、主に借入金に対して支払う金額を指す
- 例:銀行から100万円を年利5%で借りた場合、1年後に支払う利子は100万円 × 5% = 5万円
これらの用語は、金融商品の選択や投資判断を行う際に重要である。それぞれの意味と計算方法を理解することで、より適切に判断できる。

専門家のワンポイントアドバイス:
金融商品を比較する際は、税引後の実質的な利回りを確認することが大切です。
金利の基礎知識を活用した賢明な家計管理
金利の基礎知識は、日常生活のさまざまな場面で役立つ。ここでは、学んだ知識をどのように活用できるかを具体的に見ていこう。
たとえば、預金を選ぶ際には、単利と複利の違いを考慮することが大切だ。長期の資産運用なら、複利の効果が大きい商品を選ぶとよい。
ローンを組む場合、固定金利と変動金利の特徴を理解しておくことが重要である。自身の収入状況や将来の見通しに合わせて、適切な金利タイプを選択できる。
投資を検討する際には、金利と利回りの違いを意識しよう。単に高金利の商品を選ぶのではなく、リスクも考慮した総合的な判断が必要だ。
日々の家計管理でも金利の知識は役立つ。クレジットカードのリボ払いや消費者金融の利用を検討する際、年利のインパクトを理解していれば、安易な借入れを避けられる。
金融環境は常に変化している。金利の動向に注目し、必要に応じて自身の資産運用やローンの見直しを行うことが大切だ。金利の基礎知識を活かし、賢明な家計管理を心がけよう。
まとめ:金利の正しい理解が家計の健全性を支える重要な基礎知識
この記事では、金利の基礎知識について解説してきた。金利とは、お金を借りたり預けたりする際に発生する「手数料」のようなものであり、私たちの日常生活に深く関わっている。
まず、金利の基本的な仕組みと役割を学んだ。金利には時間とお金の価値を調整する役割や、お金の需要と供給のバランスを取る役割がある。
次に、利息の計算方法として単利と複利の違いを理解した。長期の資産運用では、複利の効果が大きいことがわかった。
また、預入期間と利息計算方法の関係や、金利・利回り・利子・利息といった似て非なる用語の違いについても学んだ。
これらの知識は、預金やローン、投資などの金融取引において、より賢明な判断を下すための基礎となる。日々の家計管理から長期的な資産形成まで、さまざまな場面で活用できる。
金融環境は常に変化している。ここで学んだ基礎知識をもとに、金利の動向に注目し、自身の経済状況に合わせて適切な選択をしていくことが大切だ。金利の基礎を理解し、賢明な家計管理を心がけることで、より安定した経済生活を送ることができるだろう。
- Q金利の知識は、日常生活でどのように役立ちますか?
- A
クレジットカードの選択やローンの返済計画、貯蓄や投資の方針決定など、さまざまな場面で役立ちます。例えば、クレジットカードのリボ払いの金利が高いことを理解していれば、過剰な利用を避けられます。また、住宅ローンの借り換えを検討する際にも、金利の知識は重要な判断材料となります。
- Q複利と単利では、どちらが資産形成に有利ですか?
- A
一般的に、長期の資産形成では複利の方が有利です。複利では利息が元本に加算されて再投資されるため、時間とともに資産が指数関数的に成長する可能性があります。一方、単利は元本に対してのみ利息が計算されるため、成長率は一定です。ただし、具体的にどちらが有利かは、金利の水準や投資期間によって変わってきます。
- Q金利の動向を予測するために、どのような情報を見ればよいですか?
- A
日本銀行の金融政策や、経済指標(GDP、消費者物価指数、失業率など)の動向を注視することが大切です。また、国内外の政治・経済ニュースにも目を配り、金利に影響を与える可能性のある出来事をキャッチすることが重要です。


